MAY-24 2020 Challenge

Construct Binary Search Tree from Preorder Traversal

Return the root node of a binary search tree that matches the given preorder traversal.

(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val. Also recall that a preorder traversal displays the value of the node first, then traverses node.left, then traverses node.right.)

It's guaranteed that for the given test cases there is always possible to find a binary search tree with the given requirements.

Example 1:

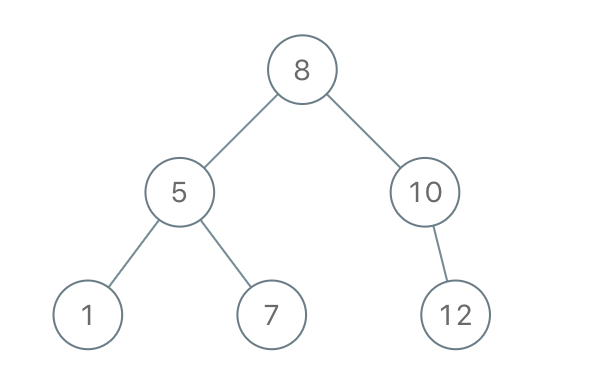
Input: [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]

Constraints:

1 <= preorder.length <= 100

1 <= preorder[i] <= 10^8

The values of preorder are distinct

Solution in Java:

class Solution {
public TreeNode bstFromPreorder(int[] preorder) {
if(preorder == null || preorder.length == 0){
return null;
}

TreeNode root = new TreeNode(preorder[0]);
Stack<TreeNode> stk = new Stack<TreeNode>();
stk.push(root);
for(int i = 1; i<preorder.length; i++){
TreeNode cur = new TreeNode(preorder[i]);
TreeNode top = stk.peek();

while(!stk.isEmpty() && stk.peek().val<preorder[i]){
top = stk.pop();
}

if(top.val < preorder[i]){
top.right = cur;
}else{
top.left = cur;
}
stk.push(cur);
}
return root;
}
}

This is simply depecting 24th Challenge of May 2020

Comments

Leetcode 371. Sum of Two Integers. C++ / Java

371 . Sum of Two Integers Given two integers a and b , return the sum of the two integers without using the operators + and - . Example 1: Input: a = 1, b = 2 Output: 3 Example 2: Input: a = 2, b = 3 Output: 5 Constraints: -1000 <= a, b <= 1000 Solution : C++ : class Solution { public: int getSum(int a, int b) { if (b==0) return a; int sum = a ^ b; int cr = (unsigned int) (a & b) << 1; return getSum(sum, cr); } }; Java : class Solution { public int getSum(int a, int b) { while(b != 0){ int tmp = (a & b) << 1; a = a ^ b; b = tmp; } return a; } } Explaination :

Leetcode 217. Contains Duplicate. Python (Easiest Approach ✅)

217 . Contains Duplicate Given an integer array nums , return true if any value appears at least twice in the array, and return false if every element is distinct. Example 1: Input: nums = [1,2,3,1] Output: true Example 2: Input: nums = [1,2,3,4] Output: false Example 3: Input: nums = [1,1,1,3,3,4,3,2,4,2] Output: true Constraints: 1 <= nums.length <= 10 5 -10 9 <= nums[i] <= 10 9 class Solution: def containsDuplicate(self, nums: List[int]) -> bool: hs = set() for n in nums: if n in hs: return True hs.add(n) return False Explaination :

Leetcode 322. Coin Change. Python (Greedy? vs DP?)

322 . Coin Change You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money. Return the fewest number of coins that you need to make up that amount . If that amount of money cannot be made up by any combination of the coins, return -1 . You may assume that you have an infinite number of each kind of coin. Example 1: Input: coins = [1,2,5], amount = 11 Output: 3 Explanation: 11 = 5 + 5 + 1 Example 2: Input: coins = [2], amount = 3 Output: -1 Example 3: Input: coins = [1], amount = 0 Output: 0 Constraints: 1 <= coins.length <= 12 1 <= coins[i] <= 2 31 - 1 0 <= amount <= 10 4 Solution : class Solution: def coinChange(self, coins: List[int], amount: int) -> int: dp = [amount + 1] * (amount + 1) #[0...7] dp[0] = 0 ...

LEETCODE SOLUTIONS

Search This Blog